Definitions
Non-Decreasing
Non-decreasing array is an array that satisfies:
arr[i + 1] >= arr[i]For example:
int arr[] = {1, 1, 1, 3, 3, 5, 6, 8, 8}Breakpoint
Here, in this article, we define an idx as a breakpoint if it satisfies:
(idx == 0 || idx[idx] > idx[idx - 1])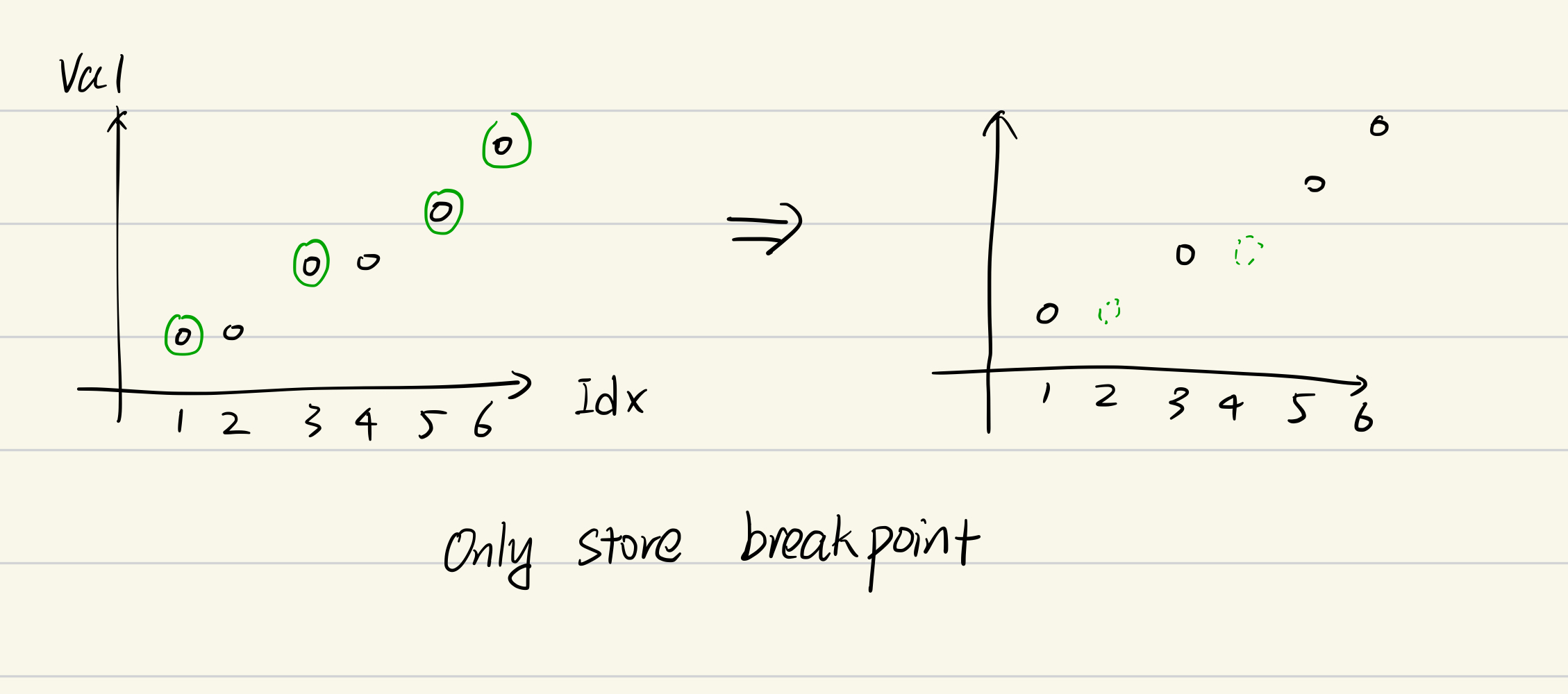
Breakpoint Info
Breakpoint Info contains the breakpoint and the value of the array element at that breakpoint:
struct BreakpointInfo {
int idx;
T value;
}Operations
Add New Breakpoint
The implementation we gave below only support adding new breakpoint that not breaking previous info. Concretely, that is:
- The
idxmust be larger or equal than any before - The
valuemust be larger then any before
Get Value At Index
Question Definition
This operation should return the actual value at an index based on that “compressed” breakpoint info. Given an targetIdx.
Based on the definition of breakpoint, we know our goal is actually to find the last element elem that satisfies:
elem.idx <= targetIdxSpecial Case
First of all, in order to promise binary search std::lower_bound return a point to a valid info, we need to promise idx in a valid range, that is:
- When
idx < 0, we modified it to0 - When
idx > maxIdx, then the last element is what we want, return directly
Binary Searching
In my implementation, I use the std::lower_bound() to find the element position res.
Lower bound function returns the first position where we could insert target without breaking the order of sequence. In a more understandable way, if we provide targetIdx, it will return the position of the first element that satisfies:
(*it).idx >= target.idx;However, based on our definition of NonDecreasingArray, we actually want to find the last element that:
(*it).idx <= target.idx;So we need an extra check:
if((*it).idx > target.idx)
it--;After this work, it now is pointing at the element we want.
Code Implementation
Non-Decreasing Array
template <typename T>
class NonDecreasingArray
{
private:
using Idx = int;
public:
struct BreakpointInfo
{
Idx idx = 0;
T value = T();
bool operator<(const BreakpointInfo &other) const
{
return idx < other.idx;
}
};
private:
vector<BreakpointInfo> mInfo;
public:
/**
* Initialize array with initial breakpoint info
*/
NonDecreasingArray()
{
mInfo.clear();
mInfo.push_back(BreakpointInfo());
}
/**
* Return the reference of last breakpoint info
*/
BreakpointInfo &getLastBreakpointInfo()
{
return mInfo.back();
}
/**
* Insert a new breakpoint into
*
* Require such breakpoint info to have:
* - larger or equal index than last addition
* - larger or equal value than last addition
*
* Otherwise, the addition opeartion will be ignored
*/
void addNewBreakpoint(Idx idx, const T &value)
{
// normalize idx
idx = std::max(0, idx);
// check if this is a valid new breakpoint info
BreakpointInfo &last = getLastBreakpointInfo();
if (idx < last.idx || value < last.value)
{
cout << "Warning: update ignored";
return;
}
// update value
if (idx == last.idx)
{
last.value = value;
}
else
{
mInfo.emplace_back(BreakpointInfo(idx, value));
}
}
/**
* return the value at target index based on breakpoint info
*/
const T &operator[](Idx targetIdx)
{
targetIdx = std::max(0, targetIdx);
BreakpointInfo &last = getLastBreakpointInfo();
if (targetIdx > last.idx)
{
return last.value;
}
BreakpointInfo target = BreakpointInfo(targetIdx, T());
auto res = std::lower_bound(mInfo.begin(), mInfo.end(), target);
const BreakpointInfo &resInfo = *res;
if (resInfo.idx > targetIdx)
{
res--;
}
return (*res).value;
}
};Usage In Real Question
Actually, we could use this custom data structure to store the DP array used in Maximum Task Value questions, checkout the code below or on Leetcode Submission page
#include <iostream>
#include <vector>
#include <algorithm>
#include <format>
using LL = long long;
using std::cout, std::endl;
using std::vector;
const bool debug = true;
template <typename T>
class NonDecreasingArray
{
private:
using Idx = int;
public:
struct BreakpointInfo
{
Idx idx = 0;
T value = T();
bool operator<(const BreakpointInfo &other) const
{
return idx < other.idx;
}
};
private:
vector<BreakpointInfo> mInfo;
public:
/**
* Initialize array with initial breakpoint info
*/
NonDecreasingArray()
{
mInfo.clear();
mInfo.push_back(BreakpointInfo());
}
/**
* Return the reference of last breakpoint info
*/
BreakpointInfo &getLastBreakpointInfo()
{
return mInfo.back();
}
/**
* Insert a new breakpoint into
*
* Require such breakpoint info to have:
* - larger or equal index than last addition
* - larger or equal value than last addition
*
* Otherwise, the addition opeartion will be ignored
*/
void addNewBreakpoint(Idx idx, const T &value)
{
// normalize idx
idx = std::max(0, idx);
// check if this is a valid new breakpoint info
BreakpointInfo &last = getLastBreakpointInfo();
if (idx < last.idx || value < last.value)
{
cout << "Warning: update ignored";
return;
}
// update value
if (idx == last.idx)
{
last.value = value;
}
else
{
mInfo.emplace_back(BreakpointInfo(idx, value));
}
}
/**
* return the value at target index based on breakpoint info
*/
const T &operator[](Idx targetIdx)
{
targetIdx = std::max(0, targetIdx);
BreakpointInfo &last = getLastBreakpointInfo();
if (targetIdx > last.idx)
{
return last.value;
}
BreakpointInfo target = BreakpointInfo(targetIdx, T());
auto res = std::lower_bound(mInfo.begin(), mInfo.end(), target);
const BreakpointInfo &resInfo = *res;
if (resInfo.idx > targetIdx)
{
res--;
}
return (*res).value;
}
};
// task struct
struct Task
{
int start;
int end;
int value;
};
// < override for task struct
bool operator<(const Task &ta, const Task &tb)
{
return ta.end < tb.end;
}
const int MAX_SIZE = 50010;
// global variables
vector<Task> tasks;
int size = 0;
// solution data
NonDecreasingArray<int> solutions[3];
void initTasks()
{
tasks.clear();
tasks.reserve(MAX_SIZE);
}
// use data in tasks array to initial layer 0 and layer 1 solutions
// also add initial (time=0, value=0) solution to layer 2
// require task to be sorted by endTime
void initSolutions()
{
auto &s = solutions;
solutions[1] = NonDecreasingArray<int>();
solutions[2] = NonDecreasingArray<int>();
// layer 1
for (const auto &t : tasks)
{
auto last = solutions[1].getLastBreakpointInfo();
if (t.value > last.value)
{
solutions[1].addNewBreakpoint(t.end, t.value);
}
}
}
void initLayer2Solution()
{
int notChoose, choose;
for (const auto &curTask : tasks)
{
notChoose = solutions[2].getLastBreakpointInfo().value;
choose = curTask.value + solutions[1][curTask.start - 1];
if (choose > notChoose)
{
solutions[2].addNewBreakpoint(curTask.end, choose);
}
}
}
class Solution
{
public:
int maxTwoEvents(vector<vector<int>> &events)
{
// init and format tasks
initTasks();
for (const auto &taskData : events)
{
tasks.emplace_back(Task(taskData[0], taskData[1], taskData[2]));
}
// sort tasks
std::sort(tasks.begin(), tasks.end());
// init solutions
initSolutions();
initLayer2Solution();
return solutions[2].getLastBreakpointInfo().value;
}
};