Minimum Cost Path with Teleportations

Thought

State Transfer Overview

State transfer for m_cost_arr[layer][r][c]:

# normal move
m_cost_arr[layer][r - 1][c]; # from above
m_cost_arr[layer][r][c - 1]; # from left
 
# teleportation
get_min_cost(
    max_teleport    = layer - 1,
    min_node_weight = weight[r][c],
)

---

In above, m_cost_arr[max_teleport][row_idx][column_idx] is a 3D array storing the dynamic programming solutions for sub-questions:

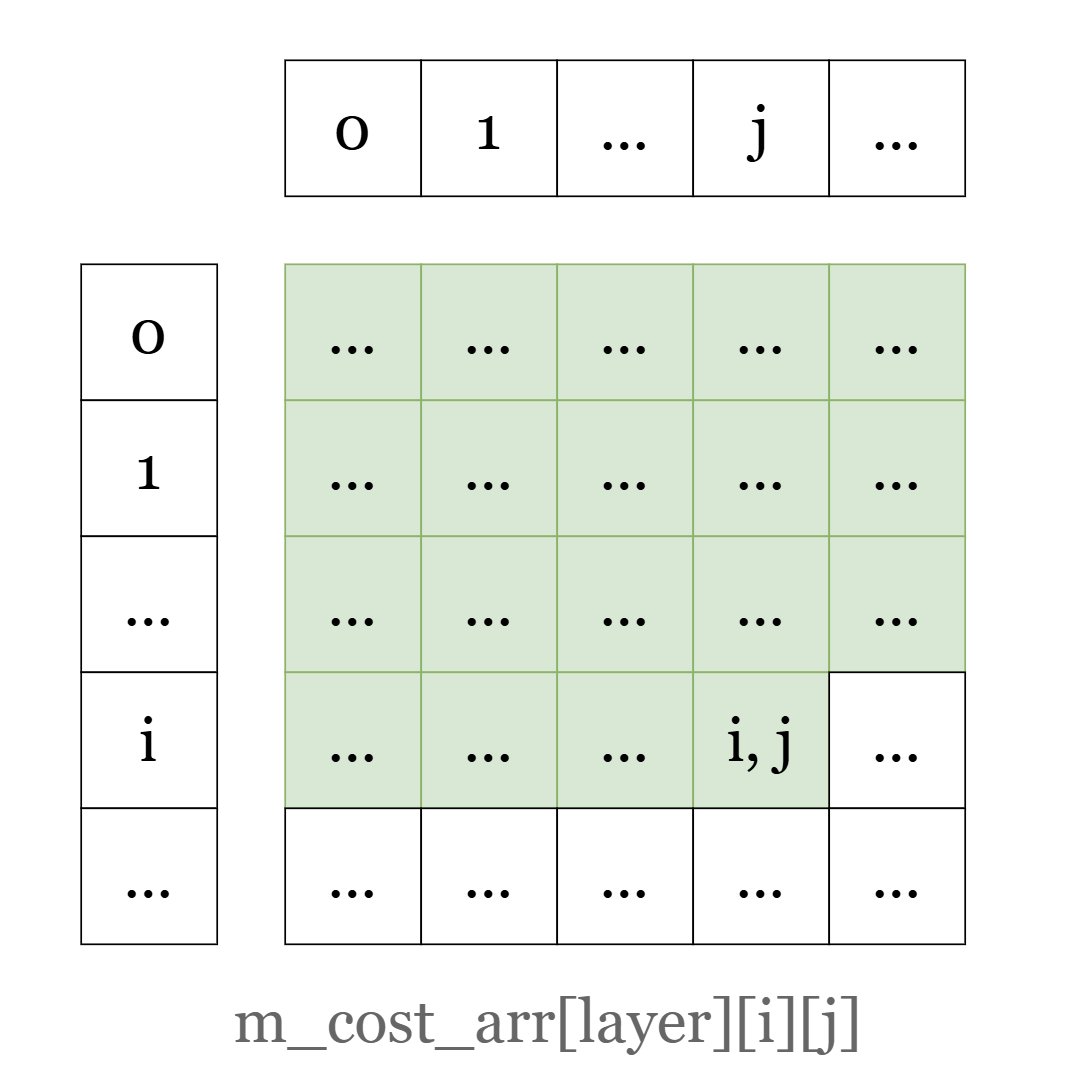
The green highlighted area is the sub-question area which’s solution stored in the array.

That is: value in m_cost_arr[layer][i][j] is the solution for sub-question when only considering highlighted nodes from $(0,0)$ to $(i,j)$ with maximum allowed transportation count layer.

Note

The sub-question area is not a strict triangular, this definition is required based on how we deal with transportation when performing state transfer. Keep reading for more info.

Note

layer in this article usually refers to max allowed transportation count.

---

We actually split up the state transfer into two different cases: The last operation to the destination point $(r,c)$:

1. Is a Normal Move operation.
2. Is a Teleportation operation.

It’s obvious that the first case could be done with $O(1)$ complexity. The point is to figure out how to perform state transfer for the second case in an efficient way, that is, the transportation as the last operation to point $(r,c)$.

Teleportation As Last Operation

We know that:

• Teleportation itself do not impose cost
• Teleportation will use teleportation quota

So we have:

  cost_from_origin_to(x, y, teleport_limit = n)
= cost_from_origin_to(i, j, teleport_limit = n - 1) + 0    # cost nothing

So the optimal solution when last operation is Teleportation should be:

$$\text{min}(\text{CostFromOriginTo}(x,y,\text{layer}-1)),\text{where: }\{\begin{array}{l}(x,y)\in \text{SubQuestionSpace}\\ \text{weight}(x,y)\ge \text{weight}(i,j)\end{array}$$

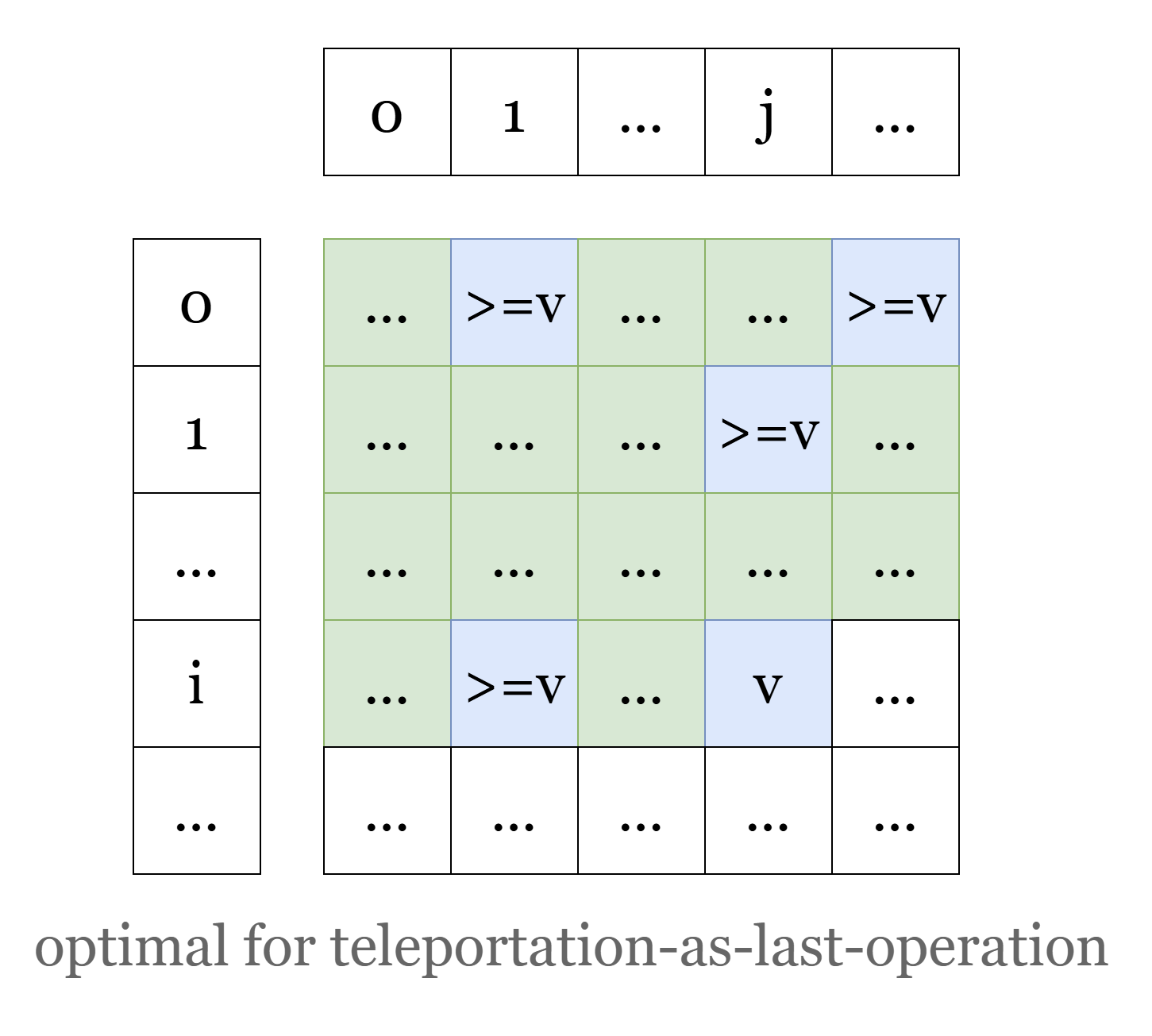For example, still consider sub-question [layer][i][j], as the image show, let’s say all the green nodes have nodes weight $<v$, and all the blue nodes have weight $\ge v$, then the optimal value for “teleportation-as-last-operation” transfer should be the min value of the sub-question of those blue-highlighted nodes in layer layer - 1.

---

To do this efficiently, we maintain one more info array:

struct MinInfo {
    weight_t weight;
    cost_t cost;
};
 
// schema: min_solution[layer] = [{weight, cost}, {weight, cost}, ...];
vector<vector<MinInfo>> min_solution;

Min Cost