Analyze

Basic Thought

For each pyramid block, the possible color (represented by one single character) is limited to following:

color = A, B, C, D, E, F

The intuitive is to use Search to iterate through the solution space (all possible value of the elements in pyramid) to find the final answer.

Searching

Store Current Search State

The the image shows below, we store the pyramid info info an 2D char array:

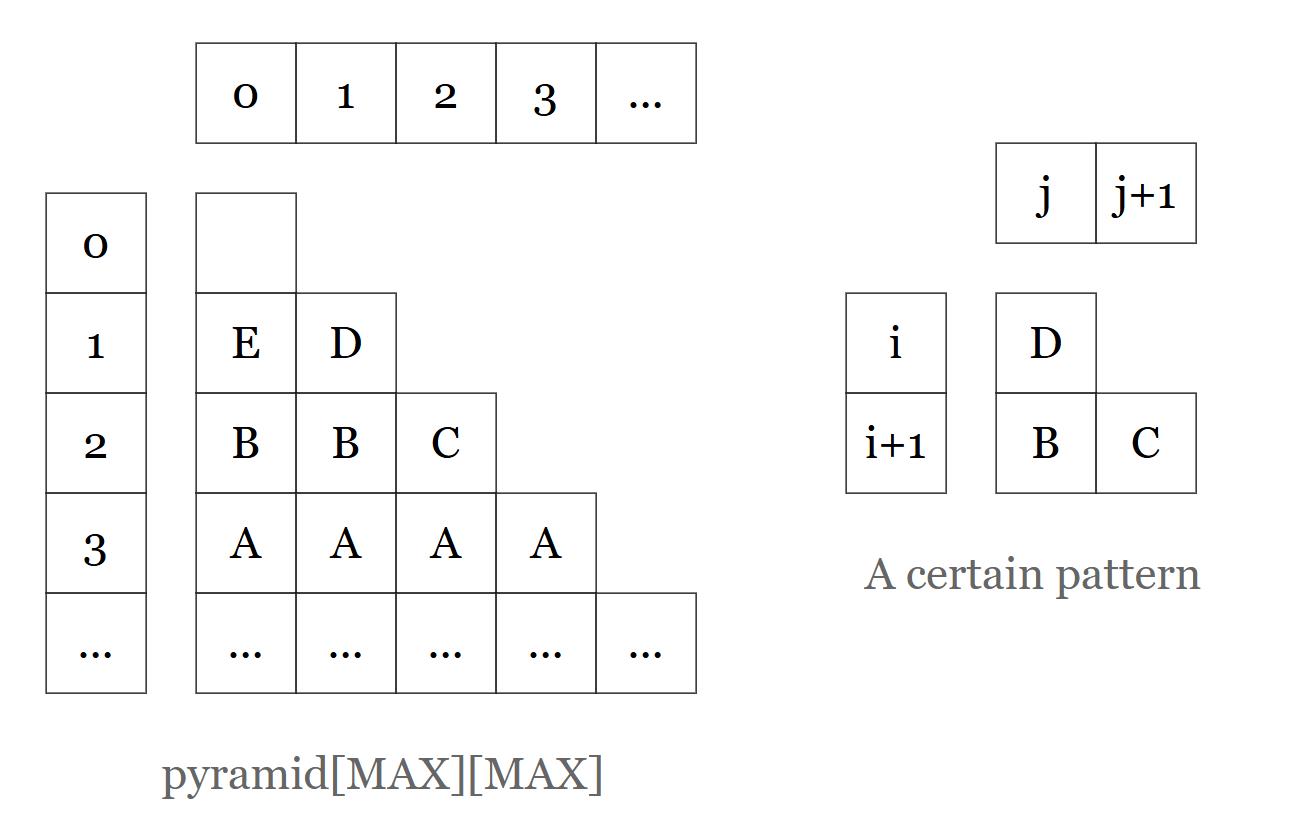
And define meaning of the value in the elements as follow:

Value	Description
`0`	Not yet searched
`[A-F]`	Searching
`1`	Searched

Search Direction

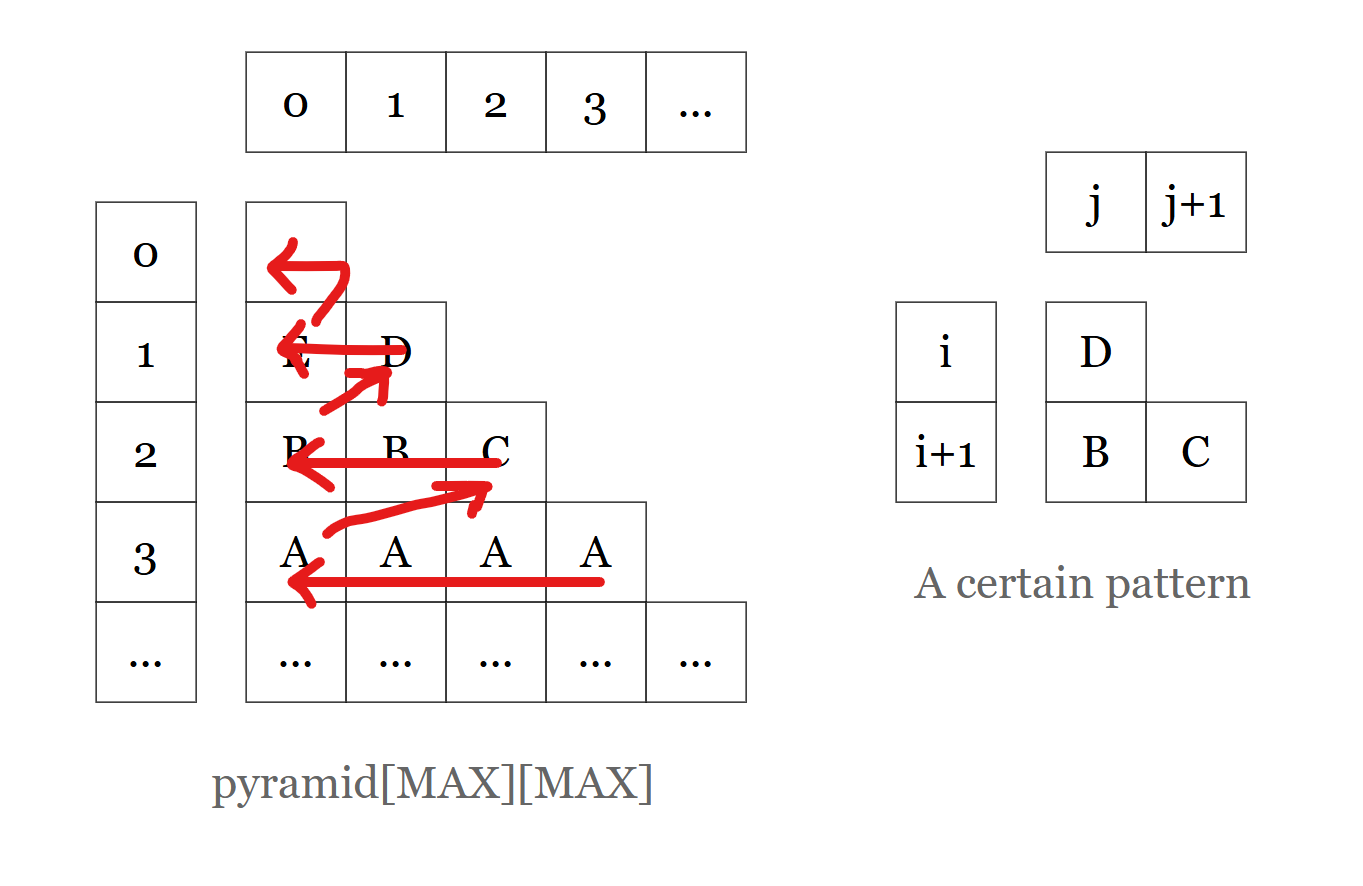
We search from right to left, from bottom to top. More concretely, consider current searching position is [curR][curC], then next search position could be calculated by code below:

def pos_forward(curR, curC):
    if(curC > 0):
        --curC   # one step left
    else:
        --curR       # search the layer above
        curC = curR  # start from right-most element

Note

Please note that all Python code in this post is intended solely to illustrate the logic and should be regarded as pseudocode.

For runnable C++ code, checkout Code Implementation sector.

Search Implementation

I decided to use a non-recursive way to implement DFS search in the solution space.

The search strategy could be explained by the code below:

def _search():
    # global variables
    global curR
    global curC
    
    # if already found valid answer, or search already finished
    # return directly
    if found or finished:
        return
 
    # search for this position is finished
    if currChar == '1':
    
        # if this is the search starting point
        # then it means the whole solution space has been searched
        if [curR, curC] == [bottom_size - 1, bottom_size - 1]:
            finished = True
            return
        
        # else, we go one step backward.
        # 
        # setting current position value to '0' is necessary, 
        # since if not doing so, next time we search this position, 
        # program will directly skip searching and go backward()
        currChar == '0'
        pos_backward()
        return
    
    # at here, the search of current position must NOT finished
    currChar = next_possible_char_for_this_pos()
    
    # this is the last position to search, and we found a valid color
    if currChar != '1' and [curR, curC] == [0, 0]:
        found = True
        return
    
    pos_forward()
 
 
def search() -> bool:
    while (not finished) and (not found):
        _search()
    
    return found

In code above:

pos_forward() / pos_backward() modify curR, curC to point to next / previous search position
next_possible_char_for_this_pos() will return next valid color character for current position based on allowed patterns and values in [curR + 1][curC] and [curR + 1][curC + 1]

def next_possible_char_for_this_pos():
    if curChar == '0':
        curChar = 'A' - 1
    
    curChar++
    
    while curChar <= 'F'
        is_valid = check_pattern(
            top=curChar, 
            bottom_left=pyramid[curR + 1][curC],
            bottom_right=pyramid[curR + 1][curC + 1],
        )
        if is_valid:
            break
    
    if curChar > 'F':
        curChar = '1'

Caching

Purely solution space searching without any cache could not pass all the testcase (due to TLE).

Therefore, we need to exploit the info produced during searching to cache some impossible answer of sub-question and use such cache in proper time.

Set Cache

We could trigger set cache when searching position change to the lower layer.

Let’s say, the position row index (or we could say, layer index) from curR = 1 to curR = 2, then at this point, we could be sure the sub question using bottom sequence as current layer 2 is impossible.

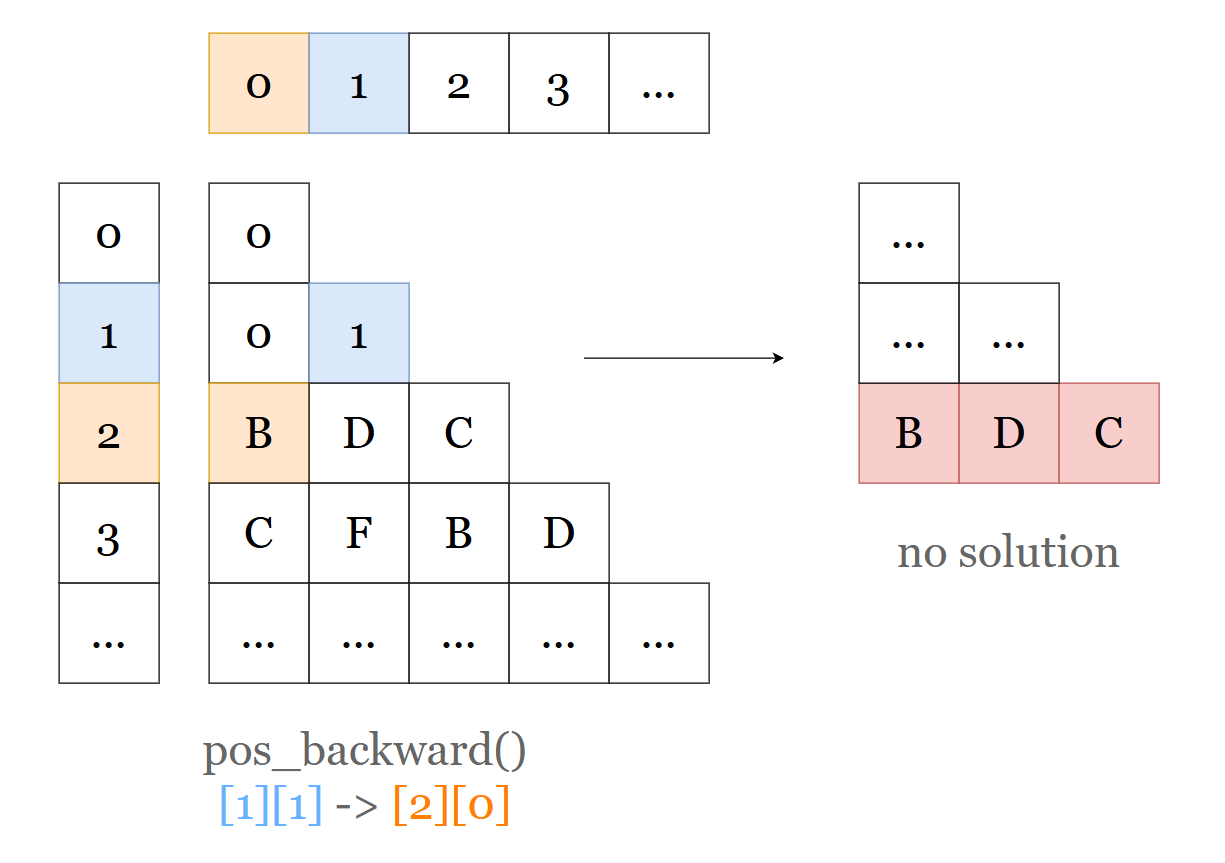
This is because, if such sub question B, D, C have solution, the search position will finally go to the curR = 0, curC = 0 and set found = 1, thus, the search is finished, and we found a valid solution for original question, and such solution use B, D, C as layer 2 elements.

Note

Here, sub question of a sequence means that: “If we could find a possible pyramid if the bottom is such sequence”.

For example, sub question using B, D, C as sequence means if we could find a valid pyramid that using B, D, C as the pyramid bottom.

Use Cache

Based on analysis above, it’s easy to know we could use cache when searching position changes to higher layer.

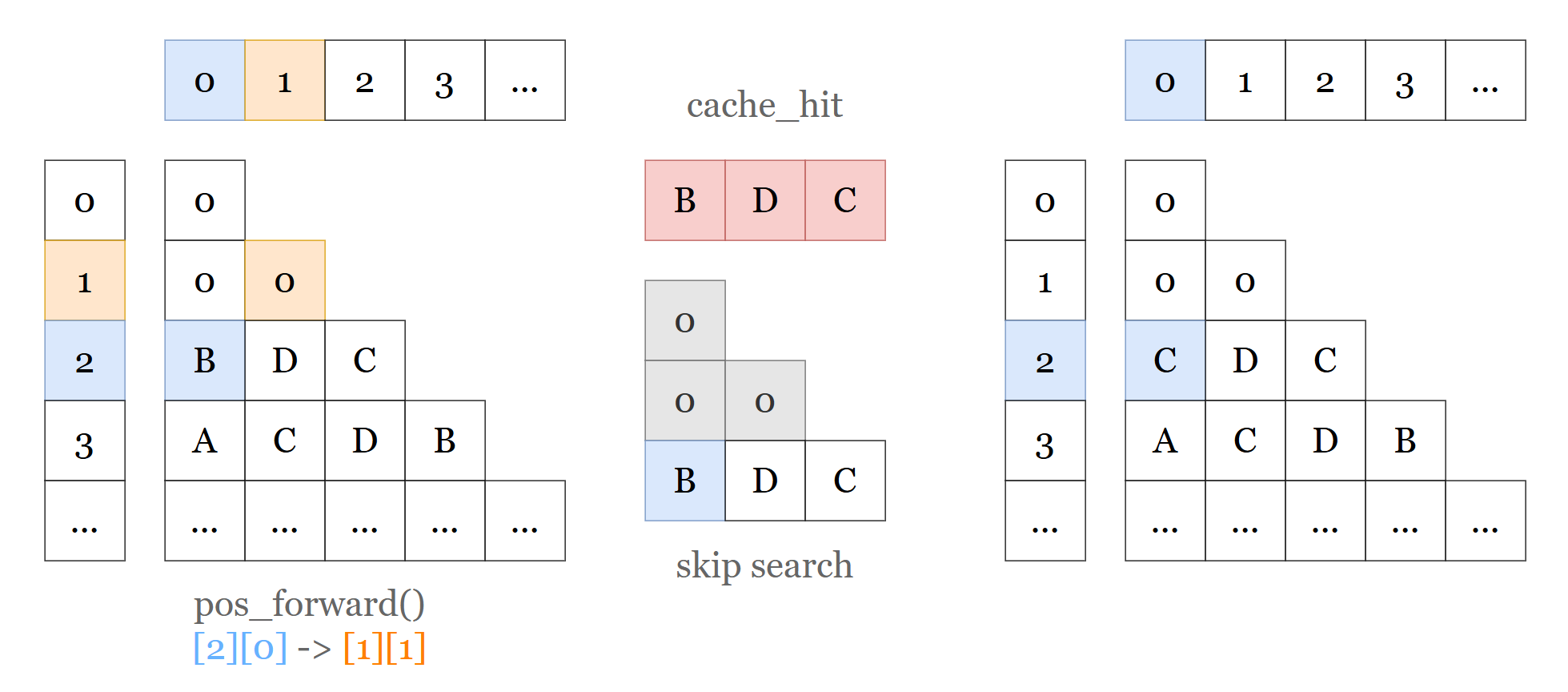
As the image above, when we goes from [2][0] to [1][1], before start searching, we first check if the sub questions of layer 2: B, D, C is in the cache.

If cache hit, it means such sub question has no solution and we should not wasting time searching further anymore. Instead, we directly go back to [2][0] again, set it to next possible value (for example from B to C in the image) then keep searching.

Note

We only need to cache the invalid sub questions, thus, the cache could be stored in a set, e.g. std::unurdered_set<std::string> cache. As long as a string sequence is in the cache (could be checked using cache.contains(str)), we can sure it doesn’t have solution.

Note

It’s easy to proof we don’t need to cache the “valid” solution of any sub question. Reusing example above, if the B, D, C sub sequence is valid as a pyramid bottom, then we will not even have a chance to cache it since the search procedure will reach the top of pyramid and declare found = true.

In other word, if any sub question is valid in our definition, it must also indicate the original question solution is also being found.

More About Cache

At the beginning, I’m actually thinking about another way of recording cache. That is, when we find a valid value for position [i][j], then if we use this position as pyramid top to consider the sub-pyramid, then all the layer should be able to considered a valid sequence as a sub question.

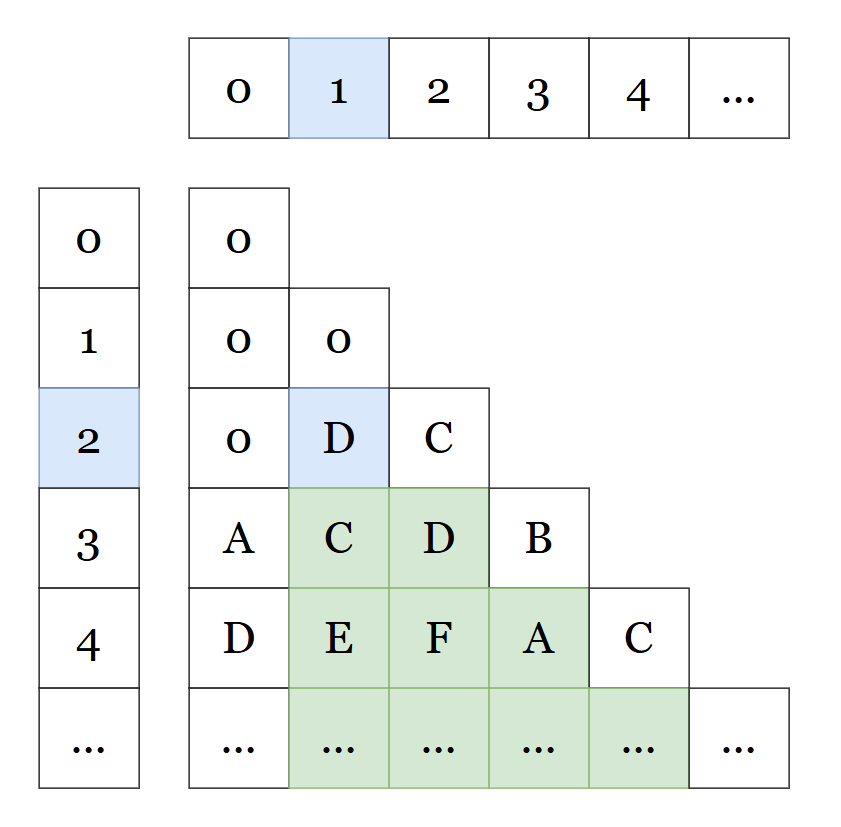
Use the image above as an example, if during the searching procedure, we found that D as a valid color for position [2][1], then we should be able to ensure the layers of the sub-pyramid are all valid sequences as sub-question, that is:

seq1 = C, D
seq2 = E, F, A
seq3 = ...

All these sequences should be consider valid, since when any of them is considered as the bottom, we could found at least a valid pyramid that satisfies the constrain of the question simply based on the sub-pyramid (the green and blue part in the image) we found.

Note

In this case, if we can not find any valid value for position [1][2], we can NOT say conversely that any layer for the sub-pyramid is not valid.

This is easy to understand, actually we could ensure C, D is not a valid pyramid bottom, however, that doesn’t mean E, F, A is not valid, since it may have other available sequence other than C, D as the upper layer of E, F, A

I tried writing solution code using this thought, triggering cache but it turns out I got TLE. The basic code logic I implement is like below:

# if we should trigger cache for current position for now?
def should_trigger_cache(curR, curC) -> bool:
    # only trigger cache when a position is being searched 
    # at the first time in current sub solution space
    if currChar != '0':
        return False
    
    # first search, but no valid value for current position
    # then do not cache
    if next_possible_char_for_this_pos() == '1':
        return False
 
    return True
 
# perform caching for all sequences of sub pyramid
def set_cache_for_sub_pyramid(curR, curC):
    for string in get_sub_pyramid_layers_as_string():
        cache.add(seq=string, value=True)

Personally I guess the cost of caching sub-pyramid for every position every time it’s first searched in a sub solution space is too high, but I can’t figure out a better approach lol

Code Implementation

#include <algorithm>
#include <format>
#include <iostream>
#include <numeric>
#include <string>
#include <unordered_set>
#include <unordered_map>
#include <vector>
 
using std::cout, std::endl;
using std::format;
using std::vector, std::string;
 
bool debug = false;
 
/**
 * Data structure to store pattern in question
 *
 * Init:
 * - Use 3-char string to init (based on questoni definition)
 * - Use three different char parameter to init
 *
 * Method:
 * - Equal comparator
 * - hash() function
 */
struct Pattern
{
    char top;
    char left;
    char right;
 
    Pattern(const string &data)
    {
        top = data[2];
        left = data[0];
        right = data[1];
    }
 
    Pattern(char top, char left, char right)
        : top(top), left(left), right(right) {}
 
    bool operator==(const Pattern &other) const
    {
        return top == other.top && left == other.left && right == other.right;
    }
 
    size_t hash() const
    {
        return std::hash<char>()(top) + std::hash<char>()(left) +
               std::hash<char>()(right);
    }
};
 
struct PatternHash
{
    size_t operator()(const Pattern &p) const { return p.hash(); }
};
 
class PatternManager
{
private:
    std::unordered_set<Pattern, PatternHash> mPatterns;
    bool mPairs[6][6];
 
public:
    PatternManager()
    {
        clear();
    }
 
    void add(const Pattern &p)
    {
        mPatterns.insert(p);
        mPairs[p.left - 'A'][p.right - 'A'] = 1;
    }
 
    bool exists(const Pattern &p)
    {
        if (!mPairs[p.left - 'A'][p.right - 'A'])
        {
            return false;
        }
        return mPatterns.find(p) != mPatterns.end();
    }
 
    void clear()
    {
        mPatterns.clear();
        for (int i = 0; i < 6; ++i)
        {
            for (int j = 0; j < 6; ++j)
            {
                mPairs[i][j] = 0;
            }
        }
    }
};
 
// global variables
// statistics
unsigned bottomSize = 0;
string bottomString;
char pyramid[6][6]; // 0: not searched, A-F: searching, 1: finished
PatternManager pMgr;
// search temp
unsigned curR, curC;
bool found, finished;
 
class AnswerCache
{
private:
    std::unordered_map<string, bool> mAllowedBottomcache;
 
    string wholeRowToString(unsigned rowIdx)
    {
        string s = "";
        for (int i = 0; i <= rowIdx; ++i)
        {
            s.push_back(pyramid[rowIdx][i]);
        }
 
        return s;
    }
 
public:
    AnswerCache() {}
 
    void setCache()
    {
        mAllowedBottomcache[wholeRowToString(curR)] = false;
    }
 
    // false: not in cache, true: hit
    int getCache(int rowIdx)
    {
        string rowStr = wholeRowToString(rowIdx);
        return mAllowedBottomcache.contains(rowStr);
    }
 
    void clear()
    {
        mAllowedBottomcache.clear();
    }
};
 
AnswerCache ansCache;
 
class Initializer
{
public:
    // init variables and clear mMgr
    void initVariables()
    {
        // init temp
        curR = bottomSize - 2;
        curC = bottomSize - 2;
        found = 0;
        finished = 0;
 
        // clear manager
        pMgr.clear();
        ansCache.clear();
 
        // clear answer cache
 
        // init pyramid
        for (int i = 0; i < 6; ++i)
        {
            for (int j = 0; j < 6; ++j)
            {
                pyramid[i][j] = '0';
            }
        }
    }
 
    // init bottomString and the pyramid array
    void initPyramidBottom(const string &data)
    {
        bottomString = data;
 
        for (int i = 0; i < bottomSize; ++i)
        {
            pyramid[bottomSize - 1][i] = data[i];
        }
    }
 
    // fill data to mMgr
    void initPattern(const vector<string> &allowed)
    {
        for (const auto &s : allowed)
        {
            pMgr.add(Pattern(s));
        }
    }
};
 
class Searcher
{
private:
    bool deltaSearchpointer(bool forward)
    {
        // forward
        if (forward)
        {
            if (curR <= 0 && curC <= 0)
            {
                return false;
            }
 
            if (curC > 0)
            {
                --curC;
            }
            else
            {
                --curR;
                curC = curR;
            }
            return true;
        }
        // backward
        else
        {
            if (curC >= bottomSize - 2 && curR >= bottomSize - 2)
            {
                return false;
            }
 
            if (curC < curR)
            {
                ++curC;
            }
            else
            {
                ++curR;
                curC = 0;
            }
            return true;
        }
    }
 
    char &curChar() { return pyramid[curR][curC]; }
 
    char &leftChar() { return pyramid[curR + 1][curC]; }
 
    char &rightChar() { return pyramid[curR + 1][curC + 1]; }
 
    bool atTop() { return curR == curC && curC == 0; }
 
    bool curValid()
    {
        return pMgr.exists(Pattern(curChar(), leftChar(), rightChar()));
    }
 
    void setToNextPossibleChar()
    {
        // search end
        if (curChar() == '1')
        {
            return;
        }
 
        // search not begin
        if (curChar() == '0')
        {
            curChar() = 'A';
            if (curValid())
            {
                return;
            }
        }
 
        ++curChar();
 
        while (curChar() <= 'F' && !curValid())
        {
            ++curChar();
        }
 
        if (curChar() > 'F')
        {
            curChar() = '1';
        }
    }
 
    void _search()
    {
 
        // already found answer
        if (found || finished)
        {
            return;
        }
 
        // try use cache to check if we could skip current layer
        // before we are about to start a new upper layer
        if (curC == curR && curChar() == '0')
        {
            if (ansCache.getCache(curR + 1))
            {
                deltaSearchpointer(0);
                return;
            }
        }
 
        setToNextPossibleChar();
 
        bool isDelta;
 
        // this position finished
        if (curChar() == '1')
        {
            isDelta = deltaSearchpointer(0);
 
            // finished
            if (!isDelta)
            {
                finished = 1;
            }
 
            // back to lower layer
            if (curC == 0)
            {
                // remember this layer of pattern doesn't work
                ansCache.setCache();
            }
            return;
        }
 
        // this position not finish searching
        isDelta = deltaSearchpointer(1);
        if (!isDelta)
        {
            found = 1;
        }
        else
        {
            curChar() = '0';
        }
        return;
    }
 
public:
    void search()
    {
        while (!found && !finished)
        {
            _search();
        }
    }
};
 
class Solution
{
public:
    bool pyramidTransition(string bottom, vector<string> &allowed)
    {
        // initialization
        bottomSize = bottom.size();
        auto initer = Initializer();
        initer.initVariables();
        initer.initPyramidBottom(bottom);
        initer.initPattern(allowed);
 
        // search the answer
        auto searcher = Searcher();
        searcher.search();
        return found;
    }
};

Oya Code Notes

Explorer

Pyramid Transition Matrix

Analyze

Basic Thought

Searching

Store Current Search State

Search Direction

Search Implementation

Caching

Set Cache

Use Cache

More About Cache

Code Implementation

Graph View

Table of Contents